Context: My capstone mentor brought up this question during a talk regarding recent AI breakthrough addressing complex system.
Professor I’ve being thinking the question for a while, I want to share some of my thoughts on it, (it’s deviate from the research and contains very long text, if you don’t have time there’s no need to read it )
I do think science is a religion (not because Newton and Einstein were religious though), in a way that it aligns with humanity’s intrinsic drive for curiosity, explanation, and rationalization.
But unlike other religions, science stands apart by constantly encouraging self-questioning and skepticism. As Max Planck might say, science progressed through the funerals.
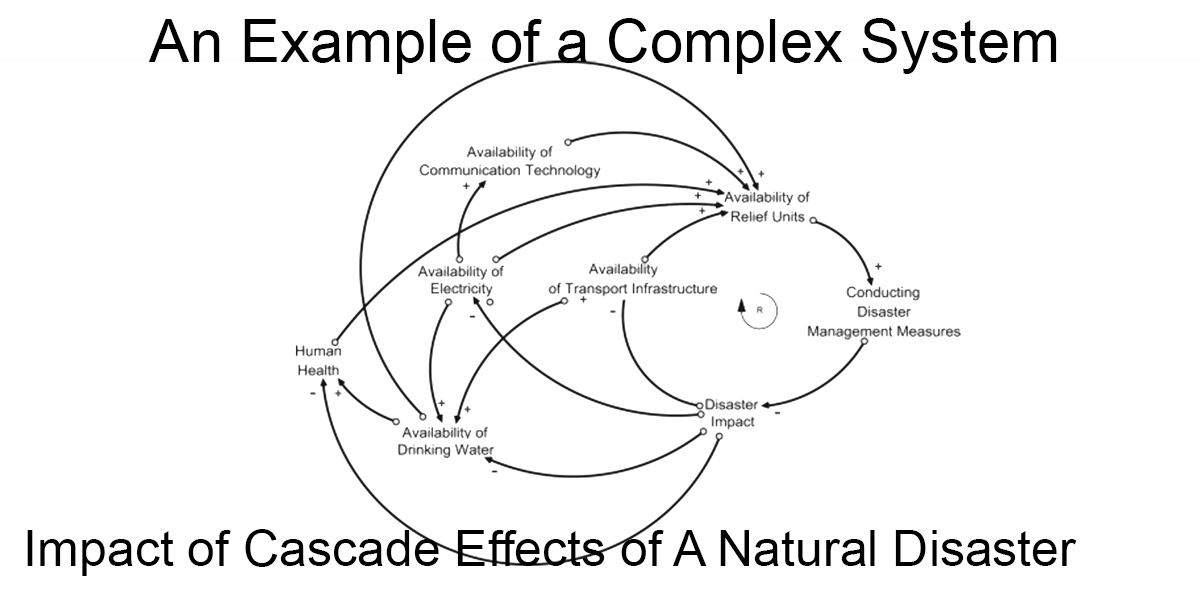
When you mentioned using deep learning to replace the traditional laws of physics, my first thought was the challenge of addressing complex systems (such as meterology) . reductionist might argue that by understanding the properties of individual components and the interactions between them, one could fully derive the behavior of the system as a whole. I personally lean towards an anti-reductionist view, which suggests otherwise. But it should be noted that although meteorology is a chaotic system that exhibits sensitivity and unpredictability, this unpredictability is fundamentally different from the uncertainty principle found in quantum mechanics. In this system, everything is, in principle, deterministic. The micro-components, such as gas molecules, have well-defined properties, and their interactions follow Newtonian laws, without involving quantum randomness. From a microscopic perspective, the weather system is entirely deterministic; however, knowing the properties of individual components does not necessarily allow us to predict the system’s overall behavior.
As a whole, the system exhibits emergent properties that cannot be deduced from its individual parts alone. In this case, relying solely on simplified physical laws often amplifies inaccuracies due to their inherent sensitivity.
This is where reductionism fails and also explains why abandoning purely reductionist approaches and instead leveraging vast computational power to analyze raw data directly can yield more accurate results. In this regard, deep learning presents a powerful challenge to the reductionist view, proving to be more effective than traditional physical laws in forecasting the behavior of chaotic systems. This anti-reductionist approach isn’t entirely new though; Philip Anderson argued in his influential 1972 Science article, “More is Different,” that complexity gives rise to fundamentally new properties that cannot be explained through reductionism alone.
complexity itself can sometimes lead to the emergence of simple, fundamental patterns. For example, in topological materials, we observe remarkably robust and simple phenomena. In the quantum Hall effect, the system’s conductivity remains quantized and independent of its shape. Similarly, in topological insulators, surface electrons behave as if they are massless, with quantized conductivity unaffected by the material’s physical form. This behavior mirrors that of a topological object, whose properties are determined not by its shape but by its topological structure. For instance, a torus retains its topological properties regardless of how it is reshaped, as long as its defining hole remains. Such “topological robustness” exemplifies resilience that supports anti-reductionist principles.
particle physics has traditionally pursued reductionist goals, aiming to identify ever-smaller fundamental particles. The term “fundamental” is applied to particles like electrons because they appear indivisible at the energy scales currently accessible. Even when subjected to higher energy collisions, these particles retain their intrinsic properties, such as the electron’s quantized charge. However, if we consider the emergent simplicity seen in complex systems like topological materials, it raises the question: could the robustness of so-called “fundamental” particles actually emerge from a deeper, more complex system that we have yet to observe? Perhaps these particles are not truly fundamental, but are instead stable, emergent entities from a more intricate underlying structure. For example, the Ginzburg-Landau theory of superconductors parallels the spontaneous symmetry breaking mechanism seen with the Higgs particle.
This line of thinking (encouraged by the deep learning and data driven approach) prompts us to reconsider the relentless pursuit of reductionism—such as constructing ever more powerful colliders to probe deeper into particle structure. I do think this shift could open up entirely new ways of understanding the universe, focusing on emergent properties within complex systems rather than simply breaking things down into their smallest components.
But I’m not sure whether the laws of physics itself should be abandoned.
It’s true that there are ongoing efforts to find a unified theory that can seamlessly combine quantum mechanics and general relativity, and many hypothesis remains untested. the newton’s law of physics break down in realms where either extremely high speeds, strong gravitational fields, or subatomic scales are involved.
In math, we rely on a set of fundamental axioms that have been established through human abstraction and logical reasoning. And Kurt Gödel used his Incompleteness Theorems demonstrated that any sufficiently powerful axiomatic system is inherently limited.
In physics, we also have fundamental laws, but unlike mathematical axioms, these laws are grounded not just in logical reasoning but in observation and empirical evidence. We often celebrate the “beauty” of these laws because they are observation-based and appear timeless—yet, realistically, we cannot know if they will hold indefinitely, as no one lives forever to confirm this. These physical laws work exceptionally well within the scales relevant to our everyday experiences, accurately explaining many phenomena.
I question whether there is truly a need to unify all these laws into a single framework, as though they should apply universally without exceptions. Perhaps it’s more like an optimization problem, where physical laws are valid only within certain constraints. They may change in the future or differ at other scales, but for now, they are excellent approximations that satisfy our current understanding and curiosity at the scales we interact with. If we were to use deep learning to replace these laws, it might solve certain problems but without truly answering the underlying questions. In this way, deep learning feels somewhat anti-curiosity—it offers solutions but doesn’t seek to understand or question why.
Throughout human history, whether through early practices like astrology, divination, rituals, or later pursuits in philosophy, science, and other fields, there seems to have always been a common thread: the quest to reduce uncertainty about the world. At its core, this pursuit is driven by our need to make life more predictable. But deep learning and neural networks, despite their impressive capabilities, are themselves riddled with uncertainty. They do not necessarily provide answers to the deeper “why” questions. It’s like a child asking if the sun will rise tomorrow and why and being told, “Yes, it will, and it will rise in the east, there’s no why”.
In overall, I think deep learning reminds us to give up on the reductionist view, but itself might not be the way for people to pursue or understand the physics.